I am currently in the process of implementing some the most cutting edge object detection algorithms here and am going to blog my experience implementing them.
This would be a great opportunity for someone not only to learn how deep learning algorithms are implemented but also informs about what it takes to get something research based like this, production ready.
In the last post , we discussed generating anchors for our image. Today, we talk about generating the target values for each anchor or what we what our model to predict for each anchor.
Calculating Targets for These Anchors
Now, that we have generated our anchors for a single image, there are two things we want the network to predict for each anchor.
-
The class of the anchor - Whether it is a background, or a particular object.
-
The modifications to the dimensions of the anchor to better fit the object - As objects in an image can be present anywhere in the image, the anchors (which are predefined crops in an image) need to be modified slightly to better fit the object.
We shall call these two things the class predictions and the bounding box offsets.
Class predictions
To calculate class predictions for an anchor, we take this anchor and all the ground truth objects as input into our function.
We want to calculate the probability of an anchor belonging to an object class. In other words , we want to place the anchor to an object class with which it overlaps the most with. If it doesn’t overlap much with any ground truth object, we place that anchor in the background class.
To calculate this degree of overlap we use IOU as the metric.
Intersection over Union (IOU)
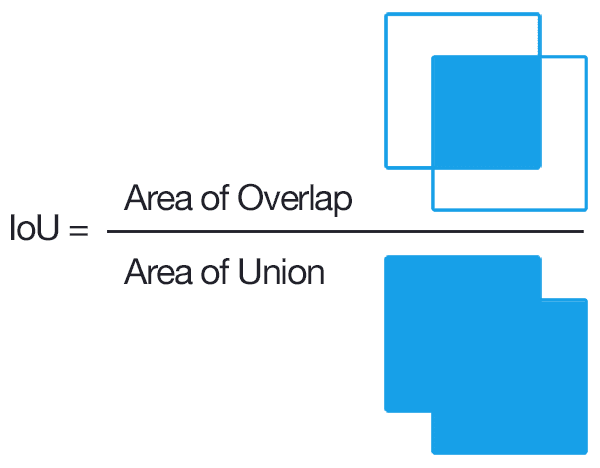
IOU provides a very nice way of measuring how much an object overlaps with another object.
We calculate IOU as follows using this function.
def calculateIOU(anchor,ob):
'''
This function calculates IOU for a two bounding boxes. This is used to
calculate the amount two boxes are similiar. Intersection over Union (IOU)
is used as the metric to calculate this.
Arguments:
1. anchor: [int,int,int,int] : Top left x,y coordinate, width and height
of anchor
2. ob : [int,int,int,int] : Top left x,y coordinate, width and height
of bounding box.
Returns:
1. iou: (float) - The intersection over union of these two boxes.
'''
assert(isinstance(anchor,list)), "The anchor sent in should be a list"
assert(isinstance(ob, list))," The bounding box/ ground truth object should be a list"
assert(len(ob) >= 4), "The length of bounding box list should be atleast 4"
assert(len(anchor) >= 4), "The length of anchor list should be atleast 4"
assert(isinstance(anchor[0],int)), "The anchor list should consist of 4 ints"
assert(isinstance(ob[0],int)), "The anchor list should consist of 4 ints"
a_x,a_y,a_w,a_h = anchor[0],anchor[1],anchor[2],anchor[3]
x,y,w,h,category = ob[0],ob[1],ob[2],ob[3],ob[4]
# getting right bottom coordinates of anchor
a_x_r = a_x + a_w
a_y_r = a_y + a_h
# getting right bottom coordinates of ground truth object
x_r = x + w
y_r = y + h
'''
Calculating overlap. One solution checks if rectangles overlap via
https://www.geeksforgeeks.org/find-two-rectangles-overlap/
If no, ,the intersection is zero.
if yes ,then intersection is calculated as in
https://www.geeksforgeeks.org/total-area-two-overlapping-rectangles/
'''
# checks If one rectangle is on left side of other or if one rectangle is
# above one another
intersection = 0
if not (a_x>x_r or x>a_x_r) and not (a_y>y_r or y>a_y_r):
# intersection is calculated if rectangles overlap
side1 = min(a_x_r,x_r) - max(a_x,x)
side2 = min(a_y_r,y_r) - max(a_y,y)
intersection = side1*side2
union = (a_h * a_w) + (h * w) - intersection
return float(intersection/union)
This function gives the IOU between two rectangular boxes.
Now, once we have this IOU metric, we can decide what class to give the anchor. A very simple notation is followed.
-
The highest IOU for an anchor and bounding box is calculated. If this IOU > 0.5 we assign the anchor the class of the corresponding bounding box.
-
If IOU with any ground truth object is less than 0.5, we assign the anchor the background class.
Hence , now each anchor has the following target data:
{
"coords": "[left top x, left top y, width, height]",
"iou": "iou_value",
"class": "class of anchor",
"offsets" : ?
}
Which brings us to calculating the offsets for the bounding boxes.
Bounding Box Offsets
As every anchor is simply a predefined crop of an image and an object can appear at any point in an image of whatever size. We need a mechanism to modify the anchor in such a way that it fits the object better.
So to do this we calculate our bounding box offsets to an anchor with the ground truth box. The Faster RCNN paper mentions a way to calculate offsets and the Yolo Papers mention another. We are currently following the Faster RCNN method. In the future, the YOLO method will be tested and the best method shall be used.
The box offsets are calculated as follows as in this function:
def calculateOffsets(anchor,ob):
'''
This function calculates the offsets for the top left x,y coordinates
and width and height of the anchor to fit the bounding box better.
The offsets are calculated as mentioned in the Faster RCNN paper.
This function is used to calculate the targets for the object detection
model.The targets are the class prediction and the bounding box offsets.
This function calculates the offsets.
Arguments:
1. anchor : ([int,int,int,int]) : The top left x,y coordinate and
width and height.
2. Ground truth object: ([int,int,int,int]) : The top left x,y
coordinate and width and height.
Returns
1. offsets: ([float,float,float,float]) : The offsets for top left x,y
coordinate and width and height.
'''
assert(isinstance(anchor,list)), "The anchor sent in should be a list"
assert(isinstance(ob, list))," The bounding box/ ground truth object should be a list"
assert(len(ob) >= 4), "The length of bounding box list should be atleast 4"
assert(len(anchor) >= 4), "The length of anchor list should be atleast 4"
assert(isinstance(anchor[0],int)), "The anchor list should consist of 4 ints"
assert(isinstance(ob[0],int)), "The anchor list should consist of 4 ints"
a_x,a_y,a_w,a_h = anchor[0],anchor[1],anchor[2],anchor[3]
x,y,w,h = ob[0],ob[1],ob[2],ob[3]
# offsets as stated by the Faster RCNN paper
t_x = (x - a_x)/a_w
t_y = (y - a_y)/a_h
t_w = math.log(w/a_w)
t_h = math.log(h/a_h)
return [t_x,t_y,t_w,t_h]
This method of finding the offsets can be broken down as follows:
Offset for x,y coordinates - (x - a_x)/a_w
We subtract the x coordinate with the anchor x coordinate and divide the whole thing by anchor width. This brings us a value that is constrained by the width of the anchor. That is if the value for the offset was 1. Then that meant that the anchor needs to be shifted to the right by a multiple of the anchor width. In this case that multiple is 1. Similarly, for the y coordinate the anchor would be needed to shifted down by a multiple of the anchor height (if the offset was positive).
Offsets for height and width - log(width/anchor_width)
The offsets for height and width are given by log(width/anchor_width) and log(height/anchor_height) respectively. Lets look at the quantity inside the log, width/anchor_width , the resultant value is constrained with the anchor_width.
The log value smoothens this value, it helps us make sense of large numbers , for more insight on why we use log refer to here link. This method is used in the code as of now.
Note
This offset calculation methodology, the anchors can be modified to be translated to any point in the image.
However, YOLO authors pointed out that this was not needed as the anchors covered all parts of the image quite well. Hence, a single anchor should only worry about modifying itself to better fit its immediate surroundings .The offsets should be constrained such that the position of the anchor should be changed within the grid cell of that anchor, and not across the whole image. The YOLO method can be read in their paper YOLOv2.
But for now, we are using the Faster RCNN formulation.